Definition Z Spread
adminse
Apr 02, 2025 · 9 min read
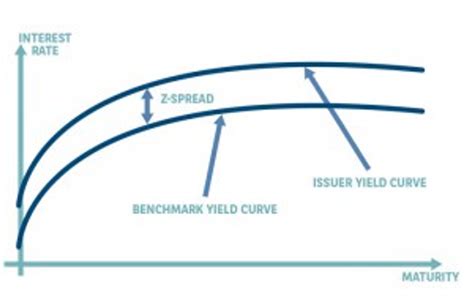
Table of Contents
Decoding the Z-Spread: A Comprehensive Guide to Understanding and Applying This Key Bond Metric
What if understanding the Z-spread unlocked a deeper understanding of bond valuation and risk assessment? This critical metric provides crucial insights into the market's perception of credit risk and liquidity premiums embedded within a bond's price.
Editor's Note: This article on the Z-spread provides a comprehensive overview of this important fixed-income metric, updated with the latest understanding and practical applications. It’s designed for finance professionals, students, and anyone seeking a deeper understanding of bond market dynamics.
Why the Z-Spread Matters: Relevance, Practical Applications, and Industry Significance
The Z-spread, a crucial metric in fixed-income analysis, offers a more accurate representation of a bond's yield than traditional measures like the yield to maturity (YTM). Unlike YTM, which assumes a flat yield curve, the Z-spread accounts for the shape of the entire Treasury yield curve, providing a more realistic picture of a bond's risk-adjusted return. Its importance stems from its ability to:
- Accurately reflect credit risk: The Z-spread incorporates the bond's credit risk, allowing investors to directly compare the yield of bonds with different credit ratings. A higher Z-spread indicates a higher perceived credit risk.
- Factor in liquidity premiums: It considers the liquidity premium, which reflects the ease or difficulty of trading a specific bond. Less liquid bonds typically have higher Z-spreads to compensate investors for the reduced trading flexibility.
- Enable better portfolio management: By utilizing Z-spreads, portfolio managers can more effectively compare bonds with different maturities and credit qualities, optimizing portfolio construction and risk management.
- Inform pricing decisions: Understanding the Z-spread facilitates more informed pricing decisions for both issuers and investors. It allows issuers to price their bonds competitively while ensuring adequate compensation for the associated risk.
Overview: What This Article Covers
This article will provide a detailed explanation of the Z-spread, starting with its definition and calculation. We'll explore its relationship to other bond yield measures, discuss its applications in various contexts, and delve into the challenges and limitations associated with its use. Finally, we'll address frequently asked questions and offer practical tips for utilizing this valuable metric.
The Research and Effort Behind the Insights
This comprehensive analysis draws upon established financial literature, including academic research papers and industry best practices. The calculation methodologies described are based on widely accepted conventions within fixed-income markets. We will also reference real-world examples to illustrate the practical applications of the Z-spread.
Key Takeaways:
- Definition and Core Concepts: A clear understanding of the Z-spread's definition, its components, and its calculation.
- Practical Applications: How the Z-spread is used in bond valuation, portfolio management, and credit risk assessment.
- Challenges and Solutions: Identifying potential limitations and discussing strategies for mitigating them.
- Future Implications: The continuing relevance of the Z-spread in the evolving landscape of fixed-income markets.
Smooth Transition to the Core Discussion
Having established the importance of the Z-spread, let's now delve into its core components and calculation methodology.
Exploring the Key Aspects of the Z-Spread
Definition and Core Concepts:
The Z-spread, also known as the zero-volatility spread, is the constant spread that must be added to each spot rate on the Treasury yield curve to make the present value of a bond's cash flows equal to its market price. In simpler terms, it represents the additional yield an investor demands to compensate for the credit risk and liquidity risk associated with a non-Treasury bond compared to a similar-maturity Treasury bond.
Calculation:
Calculating the Z-spread involves an iterative process. It requires bootstrapping the Treasury spot rate curve from available Treasury yield data. Once the spot rate curve is established, the Z-spread is found by iteratively adjusting a constant spread added to each spot rate until the discounted present value of the bond's cash flows, using the adjusted rates, equals its market price. This process typically uses numerical methods, often implemented using specialized financial software.
Applications Across Industries:
The Z-spread is widely used across various segments of the fixed-income market:
- Credit Analysis: Investment-grade and high-yield bond investors use Z-spreads to assess and compare credit risk across different bonds.
- Portfolio Management: Portfolio managers employ Z-spreads for constructing diversified portfolios, optimizing risk-adjusted returns, and conducting relative value analysis.
- Risk Management: The Z-spread provides a valuable tool for evaluating and managing interest rate and credit risks in bond portfolios.
- Derivative Pricing: Z-spreads can inform the pricing of interest rate derivatives, such as swaps and options, that are linked to the underlying bond's performance.
Challenges and Solutions:
While a powerful tool, the Z-spread has limitations:
- Data Dependency: Accurate calculation relies on a reliable and complete Treasury yield curve. Data gaps or inaccuracies can affect the accuracy of the Z-spread calculation.
- Model Risk: The specific methodology used for bootstrapping the spot rate curve and for the iterative calculation can influence the results.
- Liquidity Issues: For illiquid bonds, the observed market price may not accurately reflect the true value, leading to potentially inaccurate Z-spreads.
To address these challenges, it is crucial to use high-quality data, choose robust calculation methods, and consider the bond's liquidity when interpreting the results. Comparing Z-spreads across similar bonds mitigates some of these issues.
Impact on Innovation:
The Z-spread has driven innovation in fixed-income analytics. The demand for more precise and efficient methods of calculating Z-spreads has led to advancements in financial software and modeling techniques. Its use in risk management has prompted the development of more sophisticated risk models incorporating credit and interest rate risk.
Closing Insights: Summarizing the Core Discussion
The Z-spread stands as a crucial metric in fixed-income analysis, offering a more refined measure of a bond's yield than simpler alternatives. Its capacity to capture credit risk and liquidity premiums renders it indispensable for informed investment decisions. However, it's crucial to acknowledge the limitations and employ careful interpretation to avoid misinterpretations.
Exploring the Connection Between Option-Adjusted Spread (OAS) and the Z-Spread
The option-adjusted spread (OAS) extends the concept of the Z-spread by factoring in the embedded options within callable and putable bonds. While the Z-spread only accounts for credit and liquidity risk, the OAS further adjusts for the value of embedded options, providing a more comprehensive measure of a bond's yield. This is particularly critical for callable bonds, where the issuer has the right to redeem the bond before maturity, potentially reducing the investor's return. For putable bonds, the investor has the right to sell the bond back to the issuer, affecting the overall yield.
Key Factors to Consider:
- Roles and Real-World Examples: Consider a callable corporate bond. Its Z-spread might appear attractive, but the OAS, after accounting for the call option, could reveal a less favorable yield once the call option is factored in.
- Risks and Mitigations: Misinterpreting the Z-spread without considering the embedded option can lead to inaccurate risk assessment. Using the OAS instead provides a more realistic view of the risk-adjusted return.
- Impact and Implications: The OAS provides a more precise picture of a bond's true yield, leading to improved portfolio optimization and risk management, particularly for bonds with embedded options.
Conclusion: Reinforcing the Connection
The relationship between the Z-spread and OAS highlights the evolution of bond yield analysis. While the Z-spread offers a valuable improvement over YTM, the OAS further refines this measure by accounting for the impact of embedded options. Understanding this distinction is crucial for accurate valuation and risk management of complex bonds.
Further Analysis: Examining the OAS in Greater Detail
The OAS calculation is significantly more complex than that of the Z-spread. It requires sophisticated models that incorporate interest rate volatility and the probability of option exercise. This generally requires specialized software to determine the OAS. The OAS, unlike the Z-spread, is not a constant spread added to the spot rate curve but rather a spread that is consistently applied to model-generated forward rates.
FAQ Section: Answering Common Questions About the Z-Spread
- What is the Z-spread? The Z-spread is a constant spread added to each spot rate on the Treasury yield curve to make the present value of a bond's cash flows equal to its market price.
- How is the Z-spread different from the YTM? YTM assumes a flat yield curve, while the Z-spread considers the shape of the Treasury yield curve, providing a more accurate reflection of a bond's yield.
- What factors influence the Z-spread? Credit risk, liquidity risk, and the shape of the Treasury yield curve all significantly influence the Z-spread.
- How is the Z-spread calculated? It’s calculated through an iterative process using numerical methods that involve bootstrapping the Treasury spot rate curve and adjusting a constant spread until the present value of the bond's cash flows matches its market price.
- What are the limitations of the Z-spread? Data quality, model risk, and liquidity issues can influence the accuracy of the Z-spread.
Practical Tips: Maximizing the Benefits of the Z-Spread
- Understand the Basics: Begin by thoroughly understanding the definition and calculation methodology of the Z-spread.
- Use Reliable Data: Employ high-quality, reliable data for constructing the Treasury yield curve.
- Choose Appropriate Software: Utilize specialized financial software to efficiently and accurately calculate the Z-spread.
- Compare Across Similar Bonds: Focus on comparing Z-spreads of similar bonds to minimize the influence of data limitations and model differences.
Final Conclusion: Wrapping Up with Lasting Insights
The Z-spread provides a valuable tool for analyzing and comparing the yields of fixed-income securities. By accounting for the shape of the Treasury yield curve and incorporating credit and liquidity risks, it offers a more comprehensive and realistic assessment of a bond's risk-adjusted return compared to traditional measures. However, understanding its limitations and using it in conjunction with other analytical tools, like the OAS, is crucial for making informed investment decisions in the dynamic fixed-income market.
Latest Posts
Latest Posts
-
How To Set Up Automatic Late Fees In Quickbooks Desktop
Apr 04, 2025
-
How To Charge Late Fees In Quickbooks
Apr 04, 2025
-
How To Apply Late Fees In Quickbooks
Apr 04, 2025
-
How To Set Up Automatic Late Fees In Quickbooks Online
Apr 04, 2025
-
How Do I Set Up Automatic Late Fees In Quickbooks Desktop
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Definition Z Spread . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.