Skewness Definition In Research
adminse
Mar 28, 2025 · 8 min read
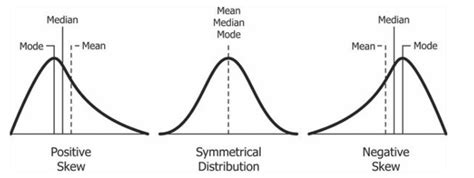
Table of Contents
Unveiling the Skew: Understanding Skewness in Research
What if the reliability of your research hinges on understanding skewness? This often-overlooked statistical concept can significantly impact the interpretation and validity of your findings.
Editor’s Note: This article on skewness in research was published today, providing researchers with up-to-date information and practical guidance on interpreting and managing skewed data.
Why Skewness Matters: Relevance, Practical Applications, and Industry Significance
Skewness, a measure of the asymmetry of a probability distribution, is a critical concept in research across various disciplines. Ignoring skewness can lead to inaccurate conclusions, flawed analyses, and ultimately, misinformed decisions. Its relevance spans numerous fields, including:
- Healthcare: Analyzing patient demographics, treatment outcomes, and disease prevalence. Skewed data in these areas can influence the design of clinical trials and the interpretation of health statistics.
- Finance: Understanding investment returns, risk assessment, and market behavior. Skewness plays a crucial role in portfolio management and risk mitigation strategies.
- Social Sciences: Examining income distribution, social inequality, and public opinion. Skewed data in these areas can influence policy decisions and social programs.
- Environmental Science: Analyzing pollution levels, climate change impacts, and ecological patterns. Understanding skewness is crucial for accurate environmental modeling and risk assessment.
Overview: What This Article Covers
This article provides a comprehensive overview of skewness in research. It will explore its definition, different types, methods of detection, impact on statistical analysis, and strategies for handling skewed data. Readers will gain a strong understanding of how to interpret and effectively manage skewness to ensure the accuracy and reliability of their research findings.
The Research and Effort Behind the Insights
This article draws upon extensive research from statistical literature, encompassing textbooks, academic journals, and online resources dedicated to statistical analysis and data interpretation. Numerous examples and case studies are included to illustrate the practical implications of skewness in real-world research settings.
Key Takeaways:
- Definition and Core Concepts: A precise explanation of skewness and its underlying principles.
- Types of Skewness: Identification and interpretation of positive, negative, and zero skewness.
- Measuring Skewness: Practical methods for quantifying skewness using statistical measures.
- Impact on Statistical Analyses: How skewness affects common statistical tests and their interpretations.
- Data Transformations: Techniques for managing skewed data to improve the validity of analyses.
- Interpreting Results: Understanding how skewness influences the overall conclusions drawn from research.
Smooth Transition to the Core Discussion:
With a foundational understanding of why skewness is vital, let's delve into its core aspects, exploring its practical implications and effective management strategies.
Exploring the Key Aspects of Skewness
Definition and Core Concepts:
Skewness quantifies the asymmetry of a probability distribution. A perfectly symmetrical distribution, like a normal distribution, has a skewness of zero. However, most real-world datasets exhibit some degree of asymmetry. This asymmetry indicates that the data points are not evenly distributed around the mean.
Types of Skewness:
-
Positive Skewness (Right Skewness): The tail of the distribution extends further to the right. The mean is typically greater than the median and mode. This suggests a concentration of data points at lower values and a few extreme values at the higher end. Examples include income distribution in many countries and house prices in specific regions.
-
Negative Skewness (Left Skewness): The tail of the distribution extends further to the left. The mean is typically less than the median and mode. This indicates a concentration of data points at higher values and a few extreme values at the lower end. Examples might include test scores where most students perform very well and a few struggle.
-
Zero Skewness: The distribution is symmetrical, with the mean, median, and mode all being approximately equal. The normal distribution is a classic example.
Measuring Skewness:
Several methods exist to measure skewness:
-
Pearson's Moment Coefficient of Skewness: This is a widely used method that calculates skewness based on the relationship between the mean, median, and standard deviation. A formula is often employed:
Skewness = 3 * (Mean - Median) / Standard Deviation. While easy to calculate, this method can be sensitive to outliers. -
Fisher-Pearson Standardized Moment Coefficient: This is a more robust version of Pearson's coefficient, less sensitive to outliers. It is often used in statistical software packages.
-
Graphical Methods: Histograms and box plots can provide visual representations of skewness. A skewed distribution will show an asymmetrical shape, with the tail extending to one side. Q-Q plots (Quantile-Quantile plots) can also help visually compare a data set’s distribution to a theoretical normal distribution.
Impact on Statistical Analyses:
Skewness significantly affects the validity and interpretation of statistical analyses. Many statistical tests, particularly parametric tests (like t-tests and ANOVA), assume a normal distribution. When data is heavily skewed, these assumptions are violated, leading to potentially inaccurate results and incorrect conclusions. For example, a t-test performed on heavily skewed data may yield a significant p-value even when there is no true effect. Non-parametric tests, which do not rely on normality assumptions, are often preferred when dealing with skewed data.
Data Transformations:
Several data transformations can be applied to reduce skewness and improve the normality of the data:
-
Log Transformation: Taking the natural logarithm (ln) of the data often reduces positive skewness. This is particularly effective when the data is positively skewed and contains a few extremely high values.
-
Square Root Transformation: Taking the square root of the data can also reduce positive skewness, although it's generally less effective than the log transformation.
-
Reciprocal Transformation: Transforming the data by taking its reciprocal (1/x) can be used for data with positive skewness and large values.
-
Box-Cox Transformation: This is a more general family of transformations that can be used to stabilize variance and normalize the distribution. It involves a parameter that needs to be estimated from the data.
Interpreting Results:
When interpreting results from analyses involving skewed data, it's crucial to consider the nature and extent of the skewness. Report the skewness measure along with descriptive statistics and note the chosen statistical tests, justifying their selection in the context of the data distribution.
Exploring the Connection Between Outliers and Skewness
Outliers, extreme data points that deviate significantly from the rest of the data, often contribute to skewness. The presence of outliers can inflate the mean, leading to a greater difference between the mean and median, and thus increasing the skewness.
Key Factors to Consider:
-
Roles and Real-World Examples: In income data, for instance, a few high-income individuals can significantly skew the distribution to the right, masking the distribution among the majority.
-
Risks and Mitigations: Ignoring outliers when analyzing skewed data can lead to inaccurate estimates of central tendency and variability. Careful consideration and potential removal (with justification) of outliers are necessary. Methods like robust statistics, which are less influenced by outliers, can also be used.
-
Impact and Implications: The misinterpretation of results due to unaccounted-for outliers and skewness can have serious consequences, leading to flawed conclusions in research and potentially incorrect policy decisions.
Conclusion: Reinforcing the Connection
The interplay between outliers and skewness highlights the importance of careful data exploration and analysis. By appropriately addressing outliers and using suitable statistical techniques, researchers can avoid biased results and draw more accurate conclusions.
Further Analysis: Examining Data Transformations in Greater Detail
Let's delve deeper into data transformations. The choice of transformation depends on the specific characteristics of the data and the goals of the analysis. For instance, the log transformation is often effective for reducing right skewness in data that is strictly positive, while the Box-Cox transformation offers a more flexible approach but requires careful consideration of the transformation parameter.
FAQ Section: Answering Common Questions About Skewness
-
Q: What is the best way to handle skewed data?
- A: The best approach depends on the severity of the skewness and the research question. Options include using non-parametric tests, applying data transformations, or employing robust statistical methods.
-
Q: How can I identify skewness in my data?
- A: Use visual tools like histograms and box plots to get an initial sense of the distribution. Calculate skewness measures (like Pearson's coefficient) for a quantitative assessment.
-
Q: What are the consequences of ignoring skewness?
- A: Ignoring skewness can lead to incorrect conclusions from statistical tests, biased estimates of central tendency and variability, and ultimately, flawed research findings.
-
Q: Are all skewed distributions problematic?
- A: Not necessarily. Mild skewness might not drastically affect the results of some analyses. However, it's crucial to assess the extent of the skewness and its potential impact on the research.
Practical Tips: Maximizing the Benefits of Understanding Skewness
-
Visualize Your Data: Always start with creating visual representations (histograms, box plots) to get a preliminary idea of your data's distribution.
-
Calculate Skewness Measures: Quantify the skewness using statistical measures like Pearson's coefficient to confirm your initial visual assessment.
-
Choose Appropriate Statistical Tests: Select statistical methods that are appropriate for the distribution of your data. Non-parametric methods are often preferred for heavily skewed data.
-
Consider Data Transformations: Explore data transformations to improve normality if parametric tests are desired. Be aware of the limitations and potential impact of each transformation.
-
Report Your Findings Clearly: Thoroughly document your data exploration, statistical methods used, and the justification behind your chosen approach.
Final Conclusion: Wrapping Up with Lasting Insights
Skewness is a crucial concept in research, representing a fundamental characteristic of many real-world datasets. Understanding its nature, its impact on statistical analyses, and the various strategies for managing it is essential for conducting reliable and valid research. By diligently addressing skewness, researchers can improve the accuracy and robustness of their findings, leading to more informed conclusions and more impactful contributions to their respective fields. The careful consideration and management of skewed data are essential for maintaining the integrity and reliability of research outcomes across all disciplines.
Latest Posts
Latest Posts
-
How To Use Forever 21 Credit Card Online
Apr 04, 2025
-
How To Check Forever 21 Credit Card Balance
Apr 04, 2025
-
How To Pay Forever 21 Credit Card Online
Apr 04, 2025
-
How To Pay Forever 21 Credit Card
Apr 04, 2025
-
How To Cancel Forever 21 Credit Card
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Skewness Definition In Research . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.