Z Definition Math
adminse
Apr 02, 2025 · 8 min read
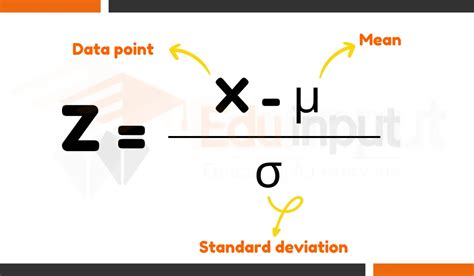
Table of Contents
Unlocking the Mysteries of Z-Definition in Mathematics: A Comprehensive Guide
What if a seemingly simple mathematical concept holds the key to unlocking complex problems across various fields? The z-definition, while often overlooked, provides a powerful framework for understanding and manipulating data, with far-reaching implications in statistics, signal processing, and beyond.
Editor’s Note: This article on the z-definition in mathematics provides a comprehensive overview of its meaning, applications, and significance. Readers will gain a practical understanding of this fundamental concept and its role in various analytical methods. Updated [Date of Publication].
Why Z-Definition Matters: Standardization, Comparison, and Beyond
The z-definition, more formally known as the z-score or standardized score, is a crucial tool in statistics and related fields. It allows for the standardization of data, enabling meaningful comparisons between different datasets with varying means and standard deviations. Understanding z-scores is critical for interpreting statistical results, conducting hypothesis testing, and understanding probability distributions. This concept finds applications in diverse areas including quality control, finance, and even social sciences, where analyzing and comparing disparate datasets is paramount.
Overview: What This Article Covers
This article delves into the core aspects of the z-definition, starting with its fundamental formula and progressing to its practical applications in various contexts. We will explore how z-scores are calculated, interpreted, and utilized to solve real-world problems. We’ll examine the importance of the standard normal distribution and its relationship to z-scores, and discuss the limitations and potential misinterpretations of z-scores.
The Research and Effort Behind the Insights
This article draws upon established statistical principles and widely accepted methodologies. Numerous textbooks, academic papers, and online resources on statistical analysis were consulted to ensure accuracy and clarity. The explanations and examples provided aim to be both rigorous and accessible to a broad audience, requiring only a basic understanding of statistical concepts.
Key Takeaways:
- Definition and Core Concepts: A precise definition of the z-score and its underlying principles.
- Calculation and Interpretation: Step-by-step guidance on calculating and interpreting z-scores.
- Applications in Statistics: Exploring the use of z-scores in hypothesis testing and confidence intervals.
- Real-World Applications: Examining practical examples across various disciplines.
- Limitations and Misinterpretations: Addressing potential pitfalls and misunderstandings surrounding z-scores.
Smooth Transition to the Core Discussion:
With a clear understanding of the z-definition's importance, let's now delve into its core aspects. We'll begin by defining the z-score and illustrating its calculation with practical examples.
Exploring the Key Aspects of Z-Definition
1. Definition and Core Concepts:
The z-score represents the number of standard deviations a data point is away from the mean of a dataset. A positive z-score indicates the data point lies above the mean, while a negative z-score indicates it lies below the mean. The formula for calculating a z-score is:
z = (x - μ) / σ
Where:
- z is the z-score
- x is the individual data point
- μ (mu) is the population mean
- σ (sigma) is the population standard deviation
If the population parameters (μ and σ) are unknown, sample statistics (mean (x̄) and standard deviation (s)) are used as estimates. This is a crucial distinction, as using sample statistics introduces sampling error and alters the interpretation slightly.
2. Calculation and Interpretation:
Let's illustrate the calculation with an example. Suppose a student scores 85 on a test where the mean score is 75 and the standard deviation is 10. The z-score would be:
z = (85 - 75) / 10 = 1
This means the student's score is one standard deviation above the mean. A z-score of -1 would indicate a score one standard deviation below the mean, and a z-score of 0 would indicate a score exactly at the mean.
3. Applications in Statistics:
Z-scores are extensively used in various statistical procedures:
- Hypothesis Testing: Z-tests are used to determine if there's a significant difference between a sample mean and a population mean.
- Confidence Intervals: Z-scores are utilized in constructing confidence intervals, providing a range of values within which the true population mean is likely to fall.
- Probability Calculations: Z-scores allow for the calculation of probabilities associated with specific data points within a normal distribution using the standard normal distribution table or statistical software.
4. Real-World Applications:
The z-definition finds applications in numerous fields:
- Quality Control: Monitoring the quality of manufactured products by comparing measurements to predetermined standards expressed as z-scores.
- Finance: Assessing investment risk and returns using z-scores to standardize performance metrics.
- Healthcare: Analyzing medical data to identify outliers and trends.
- Education: Evaluating student performance relative to a cohort using standardized scores.
5. Limitations and Misinterpretations:
It's crucial to acknowledge the limitations of z-scores:
- Assumption of Normality: Z-scores rely on the assumption that the data follows a normal distribution. If the data is significantly skewed or non-normal, the interpretation of z-scores may be misleading.
- Sensitivity to Outliers: Extreme values (outliers) can significantly influence the mean and standard deviation, impacting the calculated z-scores.
- Context is Key: The meaning of a z-score is heavily dependent on the context of the data and the specific application. A z-score of 2 might be significant in one situation but insignificant in another.
Exploring the Connection Between the Standard Normal Distribution and Z-Definition
The standard normal distribution, often denoted as N(0,1), plays a crucial role in understanding and utilizing z-scores. This distribution has a mean of 0 and a standard deviation of 1. By transforming raw data into z-scores, we effectively standardize the data, allowing us to compare it to the standard normal distribution. This allows us to use statistical tables or software to determine probabilities associated with specific z-scores. For instance, a z-score of 1.96 corresponds to a cumulative probability of approximately 0.975 in a standard normal distribution, meaning that 97.5% of the data lies below this value.
Key Factors to Consider:
-
Roles and Real-World Examples: Z-scores are used in diverse applications, including identifying outliers in datasets (e.g., detecting fraudulent credit card transactions), evaluating the performance of athletes relative to their peers (e.g., comparing Olympic athletes' scores), and assessing the efficacy of medical treatments (e.g., comparing treatment groups' success rates).
-
Risks and Mitigations: Misinterpreting z-scores due to non-normality of data is a common risk. This can be mitigated by transforming non-normal data using techniques like logarithmic transformations or employing non-parametric statistical methods. Outliers can also skew z-scores; robust statistical methods might be needed to handle these issues effectively.
-
Impact and Implications: The widespread use of z-scores impacts many decision-making processes. Understanding z-scores allows for objective comparisons and the identification of significant deviations from the norm, which can lead to better informed decisions across various domains.
Conclusion: Reinforcing the Connection
The interplay between z-scores and the standard normal distribution is fundamental to many statistical analyses. By standardizing data, z-scores enable objective comparisons, probability calculations, and hypothesis testing, providing a powerful tool for researchers and practitioners across numerous disciplines.
Further Analysis: Examining the Standard Normal Distribution in Greater Detail
The standard normal distribution’s properties, such as its symmetry around the mean and its well-defined cumulative probabilities, make it an invaluable resource in statistical analysis. Its properties are extensively documented in statistical tables and software packages. Understanding these properties enhances the accurate and effective application of z-scores. Furthermore, exploring the central limit theorem illuminates how the distribution of sample means approaches normality regardless of the underlying population distribution, strengthening the rationale behind utilizing z-scores in various statistical tests even when dealing with non-normal data under specific conditions (large sample sizes).
FAQ Section: Answering Common Questions About Z-Definition
-
What is a z-score? A z-score is a standardized score indicating how many standard deviations a data point is from the mean of its distribution.
-
How is a z-score calculated? The formula is: z = (x - μ) / σ (or z = (x - x̄) / s using sample statistics).
-
What does a positive z-score mean? A positive z-score indicates the data point is above the mean.
-
What does a negative z-score mean? A negative z-score indicates the data point is below the mean.
-
What is the standard normal distribution? The standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1.
-
When should I not use z-scores? Z-scores should be used cautiously when the data is significantly non-normal or when outliers disproportionately influence the mean and standard deviation.
Practical Tips: Maximizing the Benefits of Z-Scores
-
Verify Normality: Before using z-scores, assess whether the data reasonably approximates a normal distribution using graphical methods (histograms, Q-Q plots) or statistical tests (Shapiro-Wilk test).
-
Handle Outliers: Identify and address outliers appropriately. Consider robust statistical methods if outliers significantly impact the mean and standard deviation.
-
Interpret Contextually: Always consider the context of the data when interpreting z-scores. A z-score's significance varies depending on the application and the data's inherent variability.
-
Utilize Statistical Software: Employ statistical software to perform calculations, generate plots, and facilitate the interpretation of z-scores efficiently.
-
Understand Limitations: Acknowledge the limitations of z-scores. They do not provide a complete picture of data complexity; other descriptive and inferential statistics may be required for a comprehensive analysis.
Final Conclusion: Wrapping Up with Lasting Insights
The z-definition, while seemingly simple, provides a powerful tool for understanding, comparing, and manipulating data. By standardizing data, z-scores unlock numerous opportunities for statistical analysis, hypothesis testing, and probability calculations. However, it's crucial to interpret z-scores within their context, acknowledging their limitations and potential for misinterpretation. A thorough understanding of the z-definition empowers individuals across various disciplines to make informed decisions based on objective, standardized data.
Latest Posts
Latest Posts
-
What Is The Minimum Salary For A Credit Card In Qatar
Apr 04, 2025
-
What Is The Minimum Salary For A Credit Card In Pakistan
Apr 04, 2025
-
What Is The Minimum Salary For A Credit Card
Apr 04, 2025
-
What Is The Average Minimum Payment For A Credit Card
Apr 04, 2025
-
What Is A Minimum Payment On A Credit Card Chase
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Z Definition Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.