Z Axis Definition
adminse
Apr 02, 2025 · 8 min read
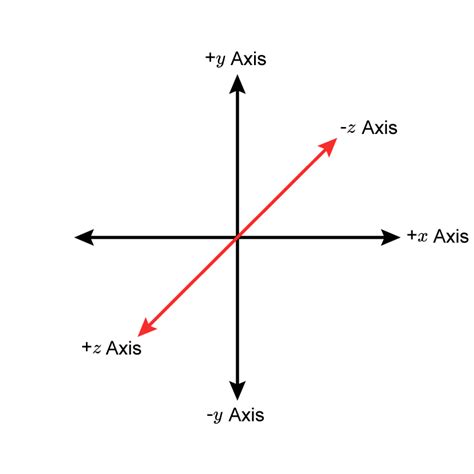
Table of Contents
Unlocking the Third Dimension: A Deep Dive into the Z-Axis Definition
What if our understanding of three-dimensional space hinges on a clear grasp of the z-axis? This fundamental concept underpins countless technologies and processes, shaping our world in profound ways.
Editor’s Note: This article on the z-axis definition was published today, providing readers with the most current and accurate information on this crucial concept in mathematics, engineering, and computer science. This exploration delves beyond basic definitions to illuminate its practical applications and significance.
Why the Z-Axis Matters: More Than Just a Coordinate
The z-axis isn't merely a line on a graph; it's the key to unlocking three-dimensional representation and manipulation. From 3D modeling and printing to robotics and medical imaging, understanding the z-axis is essential. Its relevance extends across diverse fields, impacting everything from the design of skyscrapers to the precision of surgical procedures. This article will explore its mathematical definition, its practical applications in various industries, and its crucial role in shaping our technological landscape. We'll delve into related concepts like Cartesian coordinates, right-hand rule, and its application in different software and hardware systems.
Overview: What This Article Covers
This comprehensive article systematically examines the z-axis definition. We will begin with a foundational understanding of Cartesian coordinates and the right-hand rule, proceeding to explore the z-axis in various contexts, including: its role in 3D modeling and computer graphics, its application in robotics and CNC machining, its significance in medical imaging and geographic information systems (GIS), and finally, addressing some common misconceptions and FAQs.
The Research and Effort Behind the Insights
This article is the result of extensive research, drawing upon established mathematical principles, industry documentation, and practical examples from diverse fields. Information has been synthesized from textbooks on linear algebra, computer graphics literature, engineering manuals, and online resources from reputable sources to ensure accuracy and completeness.
Key Takeaways:
- Definition and Core Concepts: A precise definition of the z-axis within the Cartesian coordinate system, including its orientation relative to the x and y axes.
- Practical Applications: Examples of the z-axis's use in various industries, such as 3D printing, robotics, and medical imaging.
- Challenges and Solutions: Addressing potential ambiguities or complexities related to the z-axis's interpretation in different systems.
- Future Implications: The continuing relevance of the z-axis in emerging technologies.
Smooth Transition to the Core Discussion
Having established the importance of understanding the z-axis, let's delve into the core concepts that underpin its definition and applications.
Exploring the Key Aspects of the Z-Axis
Definition and Core Concepts:
In a three-dimensional Cartesian coordinate system, the z-axis is one of three mutually perpendicular axes, typically represented as a vertical line. The other two axes are the x-axis (often horizontal and pointing to the right) and the y-axis (often horizontal and pointing forward). These three axes define a three-dimensional space where any point can be uniquely identified by its coordinates (x, y, z). The z-coordinate represents the point's position along the z-axis. The origin (0, 0, 0) is the point where all three axes intersect. The orientation is crucial, often determined by the right-hand rule (explained below).
The Right-Hand Rule:
The right-hand rule provides a consistent way to define the orientation of the three axes. If you curl the fingers of your right hand from the positive x-axis towards the positive y-axis, your extended thumb will point in the direction of the positive z-axis. This convention ensures consistency across different representations and systems. Inconsistency in applying the right-hand rule can lead to errors, especially in applications like robotics and 3D modeling.
Applications Across Industries:
The z-axis finds widespread application across numerous fields:
-
3D Modeling and Computer Graphics: In 3D modeling software, the z-axis dictates depth. Objects are positioned and manipulated in three dimensions, with the z-coordinate defining their distance from the viewer. This is crucial for creating realistic and interactive 3D environments. Software like Blender, Maya, and 3ds Max all rely heavily on the accurate representation and manipulation of the z-axis.
-
Robotics and CNC Machining: In robotics, the z-axis defines the vertical movement of a robotic arm or a CNC machine's cutting tool. Precise control over the z-axis is vital for tasks like welding, 3D printing, and milling. Errors in z-axis control can lead to inaccurate positioning, collisions, and damaged workpieces.
-
Medical Imaging: Medical imaging techniques like CT scans and MRI scans use a three-dimensional coordinate system. The z-axis represents the depth of the body, enabling the creation of cross-sectional images and 3D reconstructions of internal organs and structures. Precise z-axis positioning is essential for accurate diagnosis and treatment planning.
-
Geographic Information Systems (GIS): In GIS, the z-axis often represents elevation or altitude. It allows for the creation of three-dimensional maps and models of the Earth's surface, incorporating terrain data and building heights. This is crucial for applications like urban planning, environmental modeling, and navigation.
Challenges and Solutions:
While the z-axis concept is straightforward, challenges can arise in practical applications:
-
Coordinate System Variations: Different software and hardware systems might use different coordinate systems (e.g., left-handed coordinate systems). Understanding these variations is crucial to avoid errors when integrating different components or transferring data between systems.
-
Precision and Accuracy: In applications requiring high precision, such as microfabrication or surgical robotics, maintaining accuracy along the z-axis is paramount. Calibration and error correction mechanisms are essential to ensure reliable performance.
-
Data Transformation: Data often needs to be transformed between different coordinate systems. This requires careful mathematical transformations to correctly map coordinates from one system to another.
Impact on Innovation:
The z-axis plays a crucial role in continuous advancements across diverse fields. Its precise control allows for the creation of increasingly complex and sophisticated systems. For instance, advancements in 3D printing technology rely heavily on precise z-axis control for building layered structures. Similarly, robotic surgery benefits significantly from accurate z-axis manipulation to perform minimally invasive procedures.
Exploring the Connection Between Rotation and the Z-Axis
The z-axis often serves as the axis of rotation in many applications. Understanding this connection is crucial for various processes.
Key Factors to Consider:
-
Roles and Real-World Examples: In 3D modeling and gaming, rotation around the z-axis creates a spinning effect. In robotics, rotation around the z-axis allows a robotic arm to turn its end effector.
-
Risks and Mitigations: Incorrectly defining the axis of rotation can lead to unintended movements and errors. Proper calibration and software design are essential to mitigate these risks.
-
Impact and Implications: The ability to control rotation around the z-axis enables advanced functionalities in automation, simulation, and animation.
Conclusion: Reinforcing the Connection
The z-axis is not merely a mathematical abstraction; it is a fundamental element influencing countless technologies and processes. Its precise control and understanding are pivotal for innovations in 3D modeling, robotics, medical imaging, and many other fields. Errors in its understanding or implementation can have significant consequences.
Further Analysis: Examining Coordinate Transformations in Greater Detail
Coordinate transformations are essential when working with the z-axis across different coordinate systems. These involve mathematical operations to convert coordinates from one system to another. This is crucial when integrating data from various sources or transferring data between different software packages. These transformations involve matrix operations, ensuring the accurate mapping of points from one coordinate system to another. Understanding these transformations is essential for accurate 3D modeling and simulation.
FAQ Section: Answering Common Questions About the Z-Axis
Q: What is the z-axis? A: The z-axis is one of three mutually perpendicular axes in a three-dimensional Cartesian coordinate system, usually representing vertical depth.
Q: How is the z-axis defined? A: It's defined relative to the x and y axes using the right-hand rule.
Q: What is the importance of the right-hand rule? A: It establishes a consistent orientation for the coordinate system, crucial for avoiding ambiguity in applications like robotics and 3D modeling.
Q: What are some common applications of the z-axis? A: 3D modeling, computer graphics, robotics, CNC machining, medical imaging, and GIS.
Q: What are some challenges associated with using the z-axis? A: Different coordinate systems, the need for high precision, and the necessity of data transformation.
Practical Tips: Maximizing the Understanding of the Z-Axis
-
Visualize: Use visual aids and interactive 3D modeling software to understand the orientation and function of the z-axis.
-
Practice: Work through examples and exercises involving coordinate systems and transformations.
-
Consult Resources: Refer to textbooks, online tutorials, and documentation for more detailed explanations and practical examples.
Final Conclusion: Wrapping Up with Lasting Insights
The z-axis, while seemingly a simple concept, is a cornerstone of three-dimensional representation and manipulation. Its importance in shaping our technological landscape is undeniable. Understanding its definition, applications, and potential challenges is crucial for anyone working in fields that utilize three-dimensional space. The continued advancement and integration of this fundamental concept will continue to drive innovation in many sectors for years to come.
Latest Posts
Latest Posts
-
What Is The Meaning Of Liquidity Mining
Apr 03, 2025
-
Liquidity Mining Adalah
Apr 03, 2025
-
Is Liquidity Mining Profitable
Apr 03, 2025
-
Is Liquidity Mining Safe
Apr 03, 2025
-
How Does Liquidity Mining Work
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Z Axis Definition . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.