Y Coordinate Definition Math
adminse
Apr 02, 2025 · 8 min read
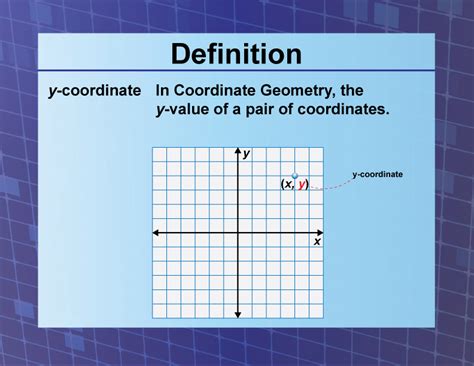
Table of Contents
Unveiling the Y-Coordinate: A Deep Dive into its Mathematical Definition and Significance
What if our understanding of space and geometry hinges on a clear grasp of the y-coordinate? This fundamental concept underpins countless mathematical applications and is crucial for navigating the world of coordinates.
Editor’s Note: This article on the y-coordinate definition in mathematics was published today, offering a comprehensive and up-to-date exploration of this essential concept. It's designed to be accessible to students and anyone seeking a deeper understanding of coordinate systems.
Why the Y-Coordinate Matters: Relevance, Practical Applications, and Industry Significance
The y-coordinate, seemingly a simple numerical value, is the cornerstone of two-dimensional and three-dimensional coordinate systems. It provides the vertical position of a point relative to a chosen reference point (origin). Its importance extends far beyond basic geometry, impacting fields like computer graphics, mapping, physics, engineering, and data visualization. Understanding the y-coordinate is essential for representing data, modelling real-world phenomena, and building complex systems. From plotting graphs to designing buildings, its applications are ubiquitous and critical. Search engines themselves rely on intricate coordinate systems to index and present information efficiently. Without a robust understanding of the y-coordinate, advancements in these fields would be significantly hindered.
Overview: What This Article Covers
This article comprehensively explores the y-coordinate, starting with its fundamental definition and progressing through its applications in various mathematical contexts. We will examine its role in Cartesian coordinates, its relationship with the x-coordinate, its extension to three dimensions (the z-coordinate), and its practical implications in diverse fields. Furthermore, we'll delve into common misconceptions and provide practical examples to solidify understanding.
The Research and Effort Behind the Insights
This article draws upon established mathematical principles, widely accepted textbooks on coordinate geometry, and numerous online resources to ensure accuracy and clarity. The information presented is vetted against standard mathematical conventions and aims to provide a reliable and comprehensive overview of the y-coordinate and its significance. The illustrative examples and explanations are designed for easy comprehension, catering to a broad range of readers.
Key Takeaways:
- Definition and Core Concepts: A precise definition of the y-coordinate within the Cartesian coordinate system.
- Two-Dimensional Applications: Exploring the role of the y-coordinate in plotting points, lines, and graphs in two dimensions.
- Three-Dimensional Extension: Understanding the y-coordinate's extension to three dimensions, forming part of a Cartesian coordinate triple (x, y, z).
- Real-World Applications: Illustrative examples showcasing the practical use of the y-coordinate in various fields.
- Common Misconceptions: Addressing and clarifying common misunderstandings related to the y-coordinate.
Smooth Transition to the Core Discussion
Having established the importance and scope of this exploration, let's now delve into a detailed examination of the y-coordinate, unraveling its intricacies and applications.
Exploring the Key Aspects of the Y-Coordinate
1. Definition and Core Concepts:
The y-coordinate is a numerical value that represents the vertical position of a point in a Cartesian coordinate system. In a two-dimensional system, a point is uniquely identified by its x- and y-coordinates, written as an ordered pair (x, y). The x-coordinate indicates the horizontal position, while the y-coordinate indicates the vertical position. The origin (0, 0) is the point where both x and y are zero. Positive y-values are above the x-axis, and negative y-values are below.
2. Applications Across Industries:
- Computer Graphics: The y-coordinate is fundamental to rendering images on a screen. Each pixel's position is determined by its x and y coordinates, allowing for precise image creation and manipulation.
- Mapping and Geographic Information Systems (GIS): Latitude, often considered a measure of north-south position, is analogous to the y-coordinate in a geographical coordinate system. GIS software heavily relies on coordinate systems to represent geographical features and spatial data.
- Physics and Engineering: The y-coordinate is crucial for describing the trajectory of projectiles, the position of objects in motion, and for designing structures and mechanical systems.
- Data Visualization: Scatter plots, line graphs, and bar charts all depend on the y-coordinate to represent the values of a variable, providing visual representations of data for analysis and interpretation.
3. Challenges and Solutions:
One potential challenge arises from the ambiguity of the coordinate system's orientation. It's crucial to clearly define the orientation of the axes (positive x to the right, positive y upwards) to avoid misinterpretations. Another challenge lies in working with different scales and units, requiring careful consideration of conversion factors to ensure accuracy. These challenges can be mitigated through clear labeling of axes, specifying units of measurement, and consistent application of mathematical principles.
4. Impact on Innovation:
The y-coordinate plays a vital, albeit often implicit, role in many technological advancements. Its precise definition and consistent application are fundamental to the functioning of GPS systems, computer-aided design (CAD) software, and numerous other technologies that rely on precise spatial representation. Improvements in computational power and algorithms continue to enhance the precision and speed of calculations involving y-coordinates, driving innovation across many sectors.
Closing Insights: Summarizing the Core Discussion
The y-coordinate is a seemingly simple yet profoundly impactful concept. Its consistent application across diverse fields underscores its fundamental importance in representing and manipulating spatial data. From plotting simple points to modeling complex physical phenomena, the y-coordinate remains a cornerstone of mathematics and its applications.
Exploring the Connection Between the X-Coordinate and the Y-Coordinate
The x- and y-coordinates are inextricably linked in the Cartesian coordinate system. They form an ordered pair (x, y) that uniquely defines a point's location in two-dimensional space. The x-coordinate provides the horizontal position, and the y-coordinate provides the vertical position, relative to the origin (0, 0). The relationship between them is orthogonal; they are perpendicular to each other. This orthogonal relationship simplifies calculations related to distance, slope, and area, forming the foundation of many geometric concepts.
Key Factors to Consider:
- Roles and Real-World Examples: The x-coordinate represents horizontal distance, while the y-coordinate represents vertical distance. Consider mapping software: longitude (analogous to x) and latitude (analogous to y) pinpoint locations on Earth.
- Risks and Mitigations: Misinterpreting the orientation of the axes can lead to errors. Clearly defining the positive and negative directions for both axes is crucial to prevent miscalculations.
- Impact and Implications: The orthogonal relationship between x and y simplifies calculations. This simplification underpins many mathematical concepts and is crucial for applications in various fields.
Conclusion: Reinforcing the Connection
The x- and y-coordinates work in tandem, forming the backbone of two-dimensional coordinate systems. Their orthogonal relationship streamlines mathematical operations and provides a robust framework for representing and manipulating spatial information across a wide range of disciplines.
Further Analysis: Examining the Cartesian Coordinate System in Greater Detail
The Cartesian coordinate system, named after René Descartes, is a fundamental tool in mathematics. Its use of perpendicular axes (x and y) to define points in a plane simplifies the representation of geometric figures and facilitates calculations related to distance, slope, and area. Extending this system to three dimensions by adding a z-axis creates a three-dimensional coordinate system, allowing for the representation of points and objects in space.
FAQ Section: Answering Common Questions About the Y-Coordinate
Q: What is the y-coordinate?
A: The y-coordinate is the vertical position of a point in a Cartesian coordinate system, represented as the second value in an ordered pair (x, y).
Q: How is the y-coordinate used in graphing?
A: In graphing, the y-coordinate determines the vertical placement of a point on a graph, alongside the x-coordinate which determines the horizontal placement.
Q: What happens if the y-coordinate is zero?
A: If the y-coordinate is zero, the point lies on the x-axis.
Q: How does the y-coordinate extend to three dimensions?
A: In three dimensions, the y-coordinate remains the vertical position, but is now part of an ordered triple (x, y, z), where z represents the depth.
Q: What are some real-world applications of the y-coordinate?
A: Real-world applications include mapping (latitude), computer graphics (pixel position), and physics (object position).
Practical Tips: Maximizing the Benefits of Understanding the Y-Coordinate
-
Visualize: Use graph paper or software to visualize points and their y-coordinates.
-
Practice: Solve problems involving plotting points, calculating distances, and finding slopes.
-
Understand context: Recognize how the y-coordinate's interpretation can vary depending on the context (e.g., geographic coordinates versus Cartesian coordinates).
Final Conclusion: Wrapping Up with Lasting Insights
The y-coordinate is a seemingly simple concept, yet it underpins a vast array of mathematical and real-world applications. A firm grasp of its definition, properties, and applications empowers individuals to effectively engage with numerous fields, from data visualization to engineering design. Its importance in creating precise spatial representations is undeniable, showcasing its continued relevance in a technologically advancing world.
Latest Posts
Latest Posts
-
What Is Liquidity Mining In Bybit
Apr 03, 2025
-
My Financial Center Byu Phone Number
Apr 03, 2025
-
My Financial Center Byu Login
Apr 03, 2025
-
My Financial Center Byu
Apr 03, 2025
-
Byu Financial Center Hours
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Y Coordinate Definition Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.