Kurtosis And Skewness Definition
adminse
Mar 28, 2025 · 8 min read
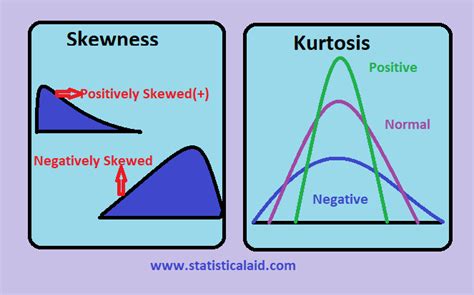
Table of Contents
Unveiling the Secrets of Kurtosis and Skewness: A Deep Dive into Data Distribution
What if a deeper understanding of kurtosis and skewness unlocked the hidden patterns within your data? These crucial statistical concepts offer invaluable insights into the shape and characteristics of your data distributions, far beyond simple averages and variances.
Editor’s Note: This comprehensive article on kurtosis and skewness provides a detailed explanation of these statistical measures, their practical applications, and how to interpret their values. We delve into their mathematical foundations and illustrate their significance with real-world examples. Updated October 26, 2023.
Why Kurtosis and Skewness Matter:
Kurtosis and skewness are descriptive statistics that go beyond the basic measures of central tendency (mean, median, mode) and dispersion (variance, standard deviation). They provide a nuanced understanding of the shape of a data distribution, revealing valuable information often missed by simpler analyses. Understanding these metrics is vital in various fields, including finance (risk assessment), healthcare (disease prevalence), engineering (quality control), and social sciences (income distribution). They allow for a more accurate interpretation of data and more informed decision-making.
Overview: What This Article Covers:
This article will provide a thorough exploration of kurtosis and skewness. We will define each concept, explore their mathematical calculations, interpret their values, and demonstrate their practical applications through real-world examples. We will also examine the relationship between kurtosis, skewness, and other statistical measures like the mean and standard deviation. Finally, we'll address frequently asked questions and offer practical tips for interpreting these crucial statistical tools.
The Research and Effort Behind the Insights:
The information presented in this article is based on extensive research, drawing from reputable statistical textbooks, academic papers, and online resources. Each concept is explained clearly and supported by relevant examples to enhance understanding. The goal is to provide a comprehensive and accessible resource for anyone interested in learning more about kurtosis and skewness.
Key Takeaways:
- Definition and Core Concepts: A precise definition of kurtosis and skewness, explaining their roles in characterizing data distributions.
- Mathematical Calculation: A step-by-step guide on how to calculate kurtosis and skewness using different methods.
- Interpreting Values: Understanding the implications of different kurtosis and skewness values, including their practical significance.
- Real-World Applications: Exploring the use of kurtosis and skewness in various fields and disciplines.
- Relationship with Other Statistics: Examining the connection between kurtosis, skewness, mean, median, and standard deviation.
- Limitations and Considerations: Addressing the potential limitations and misinterpretations of kurtosis and skewness.
Smooth Transition to the Core Discussion:
Having established the importance of understanding kurtosis and skewness, let's delve into the specifics of each concept, starting with their precise definitions and mathematical foundations.
Exploring the Key Aspects of Kurtosis and Skewness:
1. Skewness:
Skewness is a measure of the asymmetry of a probability distribution. It quantifies the extent to which a distribution is stretched or pulled in one direction. A perfectly symmetrical distribution (like a normal distribution) has a skewness of zero. Positive skewness indicates a longer tail on the right side (higher values), while negative skewness suggests a longer tail on the left (lower values).
-
Mathematical Calculation: There are several ways to calculate skewness, but the most common is the Pearson mode skewness and the Pearson median skewness. The formula for Pearson’s moment coefficient of skewness is:
Skewness = 3 * (Mean - Median) / Standard DeviationThis formula utilizes the mean, median, and standard deviation of the dataset. A more robust method, less susceptible to outliers, utilizes the third standardized moment:
Skewness = Σ[(xi - μ)³] / [(n-1)σ³]where:
xirepresents each individual data point.μrepresents the sample mean.σrepresents the sample standard deviation.nrepresents the sample size.
-
Interpreting Values:
- Skewness = 0: The distribution is perfectly symmetrical.
- Skewness > 0: The distribution is positively skewed (right-skewed). The tail on the right is longer; the mean is greater than the median.
- Skewness < 0: The distribution is negatively skewed (left-skewed). The tail on the left is longer; the mean is less than the median.
-
Real-World Applications: In finance, positive skewness in returns might be desirable (though high kurtosis might counteract this), while negative skewness in returns (potential for large losses) is less appealing. In income distribution, positive skewness indicates a concentration of wealth among a smaller percentage of the population.
2. Kurtosis:
Kurtosis measures the "tailedness" and "peakedness" of a distribution. It essentially describes the concentration of data points around the mean and in the tails. A high kurtosis distribution has heavier tails and a sharper peak than a normal distribution. A low kurtosis distribution has lighter tails and a flatter peak.
-
Mathematical Calculation: Similar to skewness, kurtosis is often calculated using the fourth standardized moment:
Kurtosis = Σ[(xi - μ)⁴] / [(n-1)σ⁴]This formula provides the excess kurtosis, which is the kurtosis minus 3. The subtraction of 3 is because the kurtosis of a normal distribution is 3. Therefore, excess kurtosis provides a comparison relative to a normal distribution.
-
Interpreting Values:
- Excess Kurtosis = 0: The distribution has the same kurtosis as a normal distribution.
- Excess Kurtosis > 0: The distribution is leptokurtic (heavy-tailed, sharp peak). There is a higher concentration of data points around the mean and in the tails.
- Excess Kurtosis < 0: The distribution is platykurtic (light-tailed, flat peak). Data points are more spread out.
-
Real-World Applications: In finance, high kurtosis in asset returns implies a higher probability of extreme events (large gains or losses). In quality control, high kurtosis might indicate a manufacturing process prone to occasional defects.
Exploring the Connection Between Standard Deviation and Kurtosis & Skewness:
Standard deviation measures the spread of data around the mean. While seemingly unrelated at first glance, standard deviation interacts subtly with kurtosis and skewness. A high standard deviation doesn't automatically imply high kurtosis or specific skewness. However, a large standard deviation can make it easier to observe skewness and kurtosis because the data is more spread out, revealing the shape of the distribution more clearly. In datasets with low standard deviation, the distribution might appear more normal even if the true kurtosis and skewness deviate from normality.
Key Factors to Consider:
- Sample Size: The accuracy of kurtosis and skewness estimates improves with larger sample sizes. Small samples can lead to unreliable results.
- Outliers: Extreme values (outliers) can significantly influence the calculation of skewness and kurtosis. Robust methods should be considered when dealing with outliers.
- Data Type: Kurtosis and skewness are primarily used for continuous data but can be adapted for discrete data.
- Interpretation Context: The interpretation of skewness and kurtosis values should always be done in the context of the specific data and the research question being addressed. A slightly positive skewness might be insignificant in one context but highly relevant in another.
Roles and Real-World Examples:
- Finance: Kurtosis is crucial for risk management, identifying potential for extreme losses ("black swan" events). Skewness helps assess the asymmetry of returns.
- Healthcare: Skewness in disease prevalence data can reveal disparities in health outcomes.
- Engineering: Kurtosis helps evaluate the consistency of manufacturing processes.
- Social Sciences: Skewness in income distribution highlights socioeconomic inequality.
Risks and Mitigations:
- Misinterpretation: Overemphasizing kurtosis and skewness without considering other aspects of the data can lead to misinterpretations.
- Data Transformations: Transforming the data (e.g., using logarithms) can sometimes reduce skewness and kurtosis, making the data more amenable to certain statistical analyses.
Impact and Implications:
Understanding kurtosis and skewness enables more accurate modeling, prediction, and informed decision-making across various fields. Ignoring these measures can lead to flawed analyses and suboptimal outcomes.
Conclusion: Reinforcing the Connection:
The relationship between standard deviation, kurtosis, and skewness is multifaceted. While standard deviation measures the spread, kurtosis and skewness paint a detailed picture of the distribution’s shape, revealing essential information about the concentration of data and potential for extreme values. The combined understanding of these descriptive statistics provides a more robust and comprehensive data analysis.
Further Analysis: Examining Outliers in Greater Detail:
Outliers are data points significantly deviating from the rest of the data. Their influence on skewness and kurtosis is considerable. Outliers can artificially inflate skewness and kurtosis, potentially misrepresenting the underlying distribution. Robust statistical methods are crucial for handling outliers effectively. Techniques like trimming (removing extreme values) or using robust estimators of skewness and kurtosis should be considered when outliers are present.
FAQ Section:
-
Q: What is the difference between kurtosis and skewness?
- A: Skewness measures the asymmetry of a distribution, indicating the direction of the longer tail. Kurtosis measures the tailedness and peakedness, showing how concentrated data is around the mean and in the tails.
-
Q: How do I choose between different methods for calculating skewness and kurtosis?
- A: The choice depends on the data's characteristics and the presence of outliers. For robust results, especially with outliers, consider methods based on standardized moments or robust estimators.
-
Q: What if my data is not normally distributed? Does it matter?
- A: Many statistical methods assume normality. Understanding skewness and kurtosis helps determine if transformations are needed to approximate normality or if non-parametric methods should be used.
-
Q: Can I use kurtosis and skewness to predict future values?
- A: Kurtosis and skewness provide insights into the likelihood of extreme events, which can inform risk assessment and forecasting. However, they don't directly predict future values.
Practical Tips:
- Visualize your data: Histograms and box plots are helpful tools for visually assessing skewness and kurtosis before calculating them numerically.
- Consider transformations: If skewness is problematic, transformations (logarithmic, square root) can sometimes normalize the data.
- Use appropriate software: Statistical software packages (R, SPSS, Python) provide functions for calculating skewness and kurtosis efficiently.
- Interpret cautiously: Avoid overinterpreting small differences in skewness and kurtosis; focus on the practical implications within the context of your data.
Final Conclusion:
Kurtosis and skewness are powerful tools for understanding data distributions beyond simple averages and spreads. By recognizing the nuances of data shape revealed by these metrics, analysts can uncover hidden patterns, make better informed decisions, and develop more accurate models. While their interpretation requires caution and consideration of various factors, a thorough understanding of kurtosis and skewness is crucial for data-driven insights in a wide range of fields.
Latest Posts
Latest Posts
-
What Is Inventory Definition Types And Examples
Apr 24, 2025
-
Inventory Write Off Definition As Journal Entry And Example
Apr 24, 2025
-
Inventory Reserve Definition Purpose And Use In Accounting
Apr 24, 2025
-
Inventory Management Defined Plus Methods And Techniques
Apr 24, 2025
-
Inventory Financing Definition How It Works Pros And Cons
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about Kurtosis And Skewness Definition . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.