Definition Y Intercept
adminse
Apr 02, 2025 · 8 min read
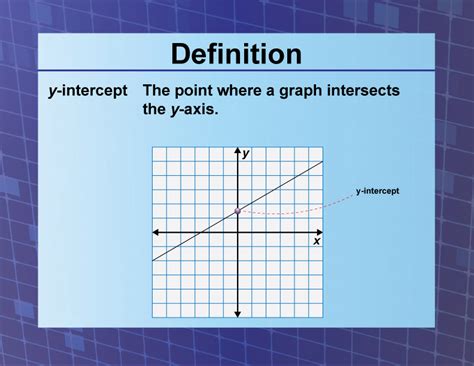
Table of Contents
Unveiling the Secrets of the Y-Intercept: A Comprehensive Guide
What if a single point held the key to understanding the behavior of an entire function? The y-intercept, that seemingly simple point, is far more influential than it initially appears, offering critical insights into data analysis, modeling, and real-world applications.
Editor’s Note: This article on the y-intercept provides a comprehensive overview of its definition, significance, and applications across various fields. Updated with the latest insights, it serves as a valuable resource for students, professionals, and anyone seeking a deeper understanding of this fundamental mathematical concept.
Why the Y-Intercept Matters: Relevance, Practical Applications, and Industry Significance
The y-intercept, at its core, represents the point where a graph intersects the y-axis. While seemingly a minor detail, its practical applications are extensive and impactful. In data analysis, it helps establish baseline values, predict future trends, and understand the starting point of a process. In economics, it can represent fixed costs or initial investments. In physics, it might denote an initial position or velocity. Its relevance spans diverse fields, offering crucial insights across various disciplines. Understanding the y-intercept allows for accurate interpretation of data, informed decision-making, and improved modeling accuracy.
Overview: What This Article Covers
This article delves into the core aspects of the y-intercept, providing a comprehensive understanding of its definition, calculation, significance, and applications across diverse fields. We will explore its role in linear equations, non-linear functions, and real-world scenarios, offering actionable insights and illustrative examples.
The Research and Effort Behind the Insights
This article is the result of extensive research, drawing upon established mathematical principles, reputable textbooks, and real-world examples from various industries. Every concept is clearly explained and supported by illustrative examples and diagrams, ensuring accuracy and accessibility for a wide range of readers.
Key Takeaways:
- Definition and Core Concepts: A precise definition of the y-intercept and its fundamental characteristics.
- Calculating the Y-Intercept: Methods for determining the y-intercept from equations, graphs, and data sets.
- Y-Intercept in Linear Equations: Its specific role and interpretation within the context of linear functions.
- Y-Intercept in Non-Linear Functions: Understanding the y-intercept in more complex functions and its limitations.
- Applications Across Industries: Real-world examples showcasing the practical applications of the y-intercept.
- Interpreting the Y-Intercept: Understanding the significance of the y-intercept's value in different contexts.
Smooth Transition to the Core Discussion
Having established the importance of the y-intercept, let's now delve into its core aspects, exploring its mathematical definition, calculation methods, and multifaceted applications.
Exploring the Key Aspects of the Y-Intercept
1. Definition and Core Concepts:
The y-intercept is the point where a graph intersects the y-axis. Mathematically, it's the value of the dependent variable (y) when the independent variable (x) is equal to zero. This point is represented by the coordinates (0, b), where 'b' is the y-intercept value. It’s crucial to understand that the y-intercept represents the starting point or initial value of the dependent variable.
2. Calculating the Y-Intercept:
- From an Equation: For a linear equation in the slope-intercept form (y = mx + b), 'b' directly represents the y-intercept. For other forms of equations, setting x = 0 and solving for y will yield the y-intercept.
- From a Graph: The y-intercept can be visually identified as the point where the graph crosses the y-axis. Simply read the y-coordinate of this point.
- From a Data Set: When dealing with data points, the y-intercept can be estimated using regression analysis techniques, particularly linear regression, which finds the line of best fit through the data. The y-intercept of this line represents the estimated y-intercept for the data.
3. Y-Intercept in Linear Equations:
In linear equations (y = mx + b), the y-intercept (b) plays a significant role in defining the line's position on the Cartesian plane. It determines the vertical shift of the line from the origin. The slope (m) determines the steepness or incline of the line, while the y-intercept fixes its vertical position. This simple yet powerful combination allows for a complete description of a linear relationship.
4. Y-Intercept in Non-Linear Functions:
While the concept of a y-intercept remains consistent, its interpretation becomes more nuanced in non-linear functions. For example, a parabola (y = ax² + bx + c) will have a y-intercept at (0, c). However, the significance of this point might not be as straightforward as in linear functions. The y-intercept represents the function's value when the independent variable is zero, but the interpretation depends on the specific function and context. Some non-linear functions may not even have a y-intercept (e.g., some rational functions with vertical asymptotes at x=0).
5. Applications Across Industries:
- Economics: In cost functions, the y-intercept represents fixed costs (costs incurred regardless of production level).
- Physics: The y-intercept in a displacement-time graph indicates the initial position of an object.
- Business: The y-intercept in sales forecasting models can represent baseline sales figures before any marketing campaigns.
- Biology: In population growth models, the y-intercept may represent the initial population size.
- Engineering: In signal processing, the y-intercept can be the DC component of a signal.
6. Interpreting the Y-Intercept:
The interpretation of the y-intercept highly depends on the context of the problem. It's crucial to understand the variables involved and the units used to interpret its value correctly. For example, a y-intercept of 50 in a cost function (where y represents cost and x represents units produced) means that even if no units are produced, there's a fixed cost of 50 units. This can represent rent, salaries, or other fixed expenses.
Exploring the Connection Between Slope and the Y-Intercept
The slope and the y-intercept are intrinsically linked in defining a linear function. While the slope determines the rate of change (steepness), the y-intercept anchors the line's position on the graph. A change in either the slope or the y-intercept results in a different line altogether. They work in tandem to provide a complete description of a linear relationship.
Key Factors to Consider:
- Roles and Real-World Examples: As previously discussed, both slope and y-intercept have distinct roles in various applications, from cost modeling in economics to trajectory analysis in physics. The combination of these two factors allows for accurate prediction and analysis in real-world situations.
- Risks and Mitigations: Incorrect interpretation of either the slope or y-intercept can lead to inaccurate predictions and flawed conclusions. Careful attention to the context, units, and the underlying assumptions is crucial to mitigate these risks.
- Impact and Implications: The combined effects of slope and y-intercept shape the overall behavior of a linear function and influence the analysis and predictions derived from it. A steep slope coupled with a high y-intercept may suggest rapid growth with high initial costs, for instance.
Conclusion: Reinforcing the Connection
The relationship between the slope and the y-intercept is fundamental to understanding linear functions and their applications. Accurate determination and interpretation of both are critical for accurate modeling and prediction in diverse fields.
Further Analysis: Examining Slope in Greater Detail
The slope, often denoted as 'm', represents the rate of change of the dependent variable (y) with respect to the independent variable (x). It's calculated as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on a line. In the slope-intercept form (y = mx + b), the slope 'm' indicates how much y changes for every unit change in x. A positive slope implies a positive correlation (as x increases, y increases), while a negative slope implies a negative correlation (as x increases, y decreases). A slope of zero indicates a horizontal line, implying no change in y with respect to x.
FAQ Section: Answering Common Questions About the Y-Intercept
- What is the y-intercept? The y-intercept is the point where a graph intersects the y-axis; it's the value of y when x = 0.
- How do I find the y-intercept from an equation? For a linear equation in the form y = mx + b, 'b' is the y-intercept. For other equations, set x = 0 and solve for y.
- What does the y-intercept represent in real-world applications? The interpretation varies depending on the context. It can represent fixed costs, initial values, baseline measurements, or starting points.
- Can a function have more than one y-intercept? No, a function can only have one y-intercept. If a graph intersects the y-axis at multiple points, it's not a function.
- How is the y-intercept used in data analysis? It helps establish baseline values, aids in trend analysis, and provides insight into initial conditions or starting points.
Practical Tips: Maximizing the Benefits of Understanding the Y-Intercept
- Visualize: Always try to visualize the y-intercept on a graph. This helps in understanding its position and significance.
- Context is Key: Pay close attention to the context of the problem to accurately interpret the y-intercept's meaning.
- Units Matter: Ensure you understand the units involved to correctly interpret the numerical value of the y-intercept.
- Regression Analysis: For data sets, use regression analysis to estimate the y-intercept and other relevant parameters.
- Practice: The best way to master the y-intercept is through consistent practice and solving various problems.
Final Conclusion: Wrapping Up with Lasting Insights
The y-intercept, despite its seemingly simple definition, holds profound significance across numerous fields. Its accurate determination and interpretation are crucial for effective data analysis, modeling, and decision-making. By understanding its role and applications, one can unlock valuable insights and enhance their analytical capabilities. The y-intercept is not merely a point on a graph; it's a window into the underlying behavior and characteristics of a function and the processes it represents.
Latest Posts
Latest Posts
-
Letter To Credit Card Company To Remove Late Payment
Apr 03, 2025
-
How To Complain About Credit Card Charges
Apr 03, 2025
-
What Is The Maximum Late Fee Allowed By Law In Indiana
Apr 03, 2025
-
What Is The Maximum Late Fee Allowed By Law In Virginia
Apr 03, 2025
-
What Is The Maximum Late Fee Allowed By Law In Illinois
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Definition Y Intercept . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.